Metropolis-Hastings Algorithm for MCMC

This is a quick overview of how to implement a version of Metropolis-Hastings (MH) algorithm for Markov Chain Monte Carlo (MCMC) for Bayesian inference.

Model Specification

Define a model of observed data (y) normally independently and identically distributed. Assigning prior distributions over the population parameters of interest for the mean μ and variance σ2 drawn from Normal and Inverse-Gamma distributions, respectively.

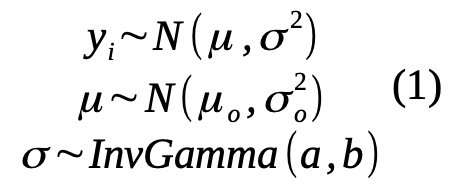
The probability model that infers the population parameters of interest and assuming independence between the population parameters implied above

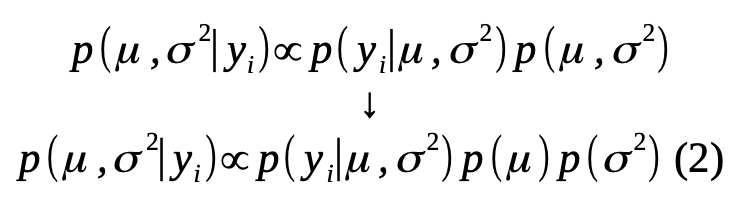
The likelihood of the parameters conditioned on all the data is the product of the probability distribution for each data point and the probability of the parameters of interest conditioned on their prior distributions. In numeric computation, calculating probabilities on the natural-log scale reduces round-off and underflow errors, so the likelihood and the more practical log transformation of the likelihood is

Metropolis Random-walk

The generic Metropolis-Hastings algorithm approximates a parameter’s probability distribution by generating a Markov chain from a proposal distribution q as follows:

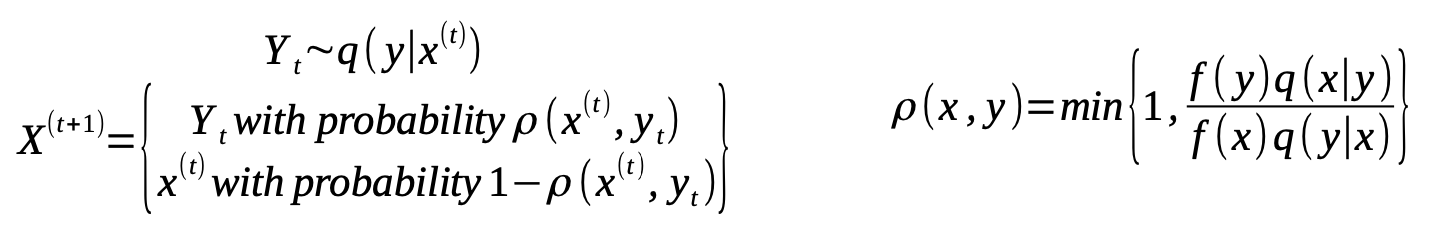
A Metropolis random walk simplifies the random draw step by assuming using a proposal distribution that is symmetrically drawn from the current value of the chain, for instance using a Normal distribution.

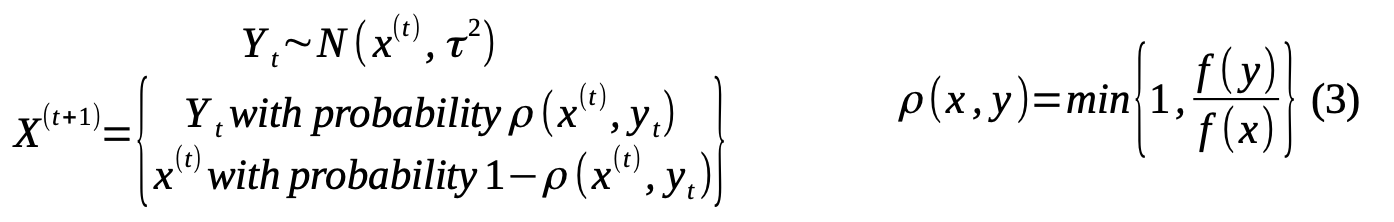
Finally, given the probability of acceptance, we randomly sample u~Uniform(0,1) and accept if ρ is grater than u. The parameter τ determines how broad the random jump may be from the current value, and should be selected such that acceptance rates aren’t too low nor too high.